问题提出

市场上有n种资产 S (i=1,2,...,n)可以选择作为投资项目，现用数额为M的相当大的资金作一个时

期的投资。这n种资产在这一时期内购买$S_i$的平均收益率为$r_i$,风险损失率为$q_\mathrm{i}$。投资越分散，总的风险越小，总体风险可用投资的$S_i$中最大的一个风险来度量。

购买$S_i$要付交易费(费率$p_i$),当购买额不超过给定值$u_i$时，交易费按购买$u_i$计算。另外，假定同期银行存款利率是$\mathbf{r}_0(\mathbf{r}_0=5\%)$,既无交易费又无风险费。

已知n=4时相关数据如下：

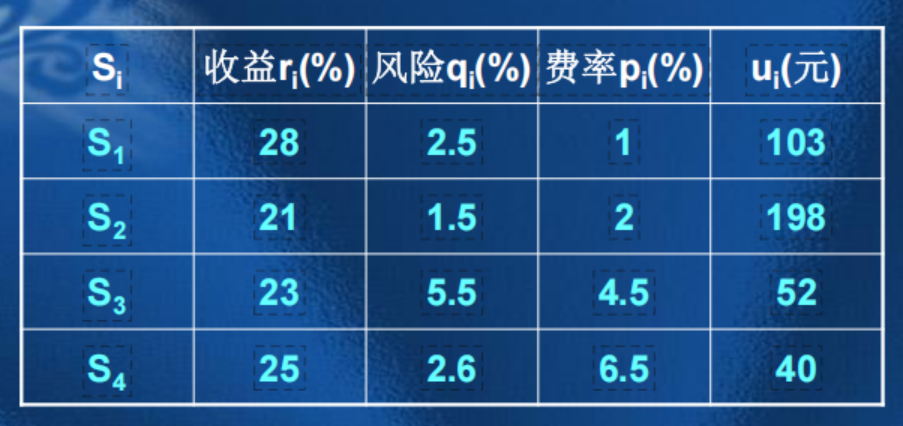
请给该公司设计一种投资组合方案，即用给定的资金M，有选择地购买若干种资产或存银行生息，使净收益尽可能大，且总体风险尽可能小。

类似模型一，求解模型二：固定盈利水平，优化风险。并根据结果分析参数k的选取。k的取值：[0,0.27]，每隔0.001求解一个相应的线性规划问题，记录相应的最优值和最优解。画出k与最优解R对应的散点图。指出k取何值时，模型最为合适，R的值最小。

问题假设

投资数额 M 相当大，为了便于计算，假设 M=1。

投资越分散，总的风险越小。

总体风险用投资风险中 $S_i$ 最大的一个风险来度量。

N 种资产 $S_i$之间是相互独立的。在投资的这一时期内，$r_i,q_i,p_i,r_0$为定值，不受意外因素的影响。净收益和总体风险只受$r_i,q_i,p_i$ 影响，不受其他因素干扰。

模型符号

$\begin{aligned} & S_{i} & & \text{第i种投资项目,如股票,债券等}\\ & r_{i_{}} & & \text{第i种投资项目的平均收益率}\\ & q_{i} & & \text{第i种投资项目的风险损失率}\\ & p_{i} & & \text{第i种投资项目的交易费率}\\ & u_{i} & & \text{第i种投资项目的交易定额}\\ & x_{i} & & \text{第i种投资项目的投资金额}\\ & r_0 & & \text{同期银行利率}\\ & \alpha & & \text{投资风险度}\\ & Q & & \text{总体收益}\\ & \Delta Q & & \text{总体收益的增量}\end{aligned}$

模型建立：

投资者希望找到总盈利至少达到水平k以上，优化到风险最小的投资方案。这样就把多目标变成一个目标的线性规划。

决策变量：

$x_i$

目标函数：

$$
\operatorname*{\mathrm{min}}R=\operatorname*{\mathrm{min}}{\operatorname*{\left\lbrace\mathrm{max}\{q_{i}x_{i},i=0,1\ldots n\}\right\rbrace}}
$$

约束条件：

$$
\sum_{i=0}^{n}(r_{i}-p_{i})x_{i}\geq k
$$

$$
\sum_{1=0}^{n}(1+p_{i})x_{i}=M
$$

$$
x_{i}\geq0,i=0,1,...n
$$

模型求解

把上述题目数据代入公式：

$$
\operatorname*{\mathrm{min}}R=\operatorname*{\mathrm{min}}{\operatorname*{\left\lbrace\mathrm{max}\{q_{i}x_{i},i=0,1\ldots n\}\right\rbrace}}
$$

$$
s.t.\begin{cases}0.05x_0+0.27x_1+0.19x_2+0.185x_3+0.185x_4\geq k\\x_0+1.01x_1+1.02x_2+1.045x_3+1.065x_4=M\\x_i\geq0,i=0,1,2,3,4\end{cases}
$$

import numpy as np
import scipy.optimize as opt
import matplotlib.pyplot as plt

# 配置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体字体
plt.rcParams['axes.unicode_minus'] = False  # 正常显示负号

# 定义目标函数和约束
def objective(x, q):
    return np.max(q * x)

def constraint_1(x, k):
    # 盈利约束
    return np.dot([0.05, 0.27, 0.19, 0.185, 0.185], x) - k

def constraint_2(x):
    # 资金约束
    return np.dot([1, 1.01, 1.02, 1.045, 1.065], x) - 1

# 初始化参数
q = np.array([0, 0.025, 0.015, 0.055, 0.026])  # 各资产的风险损失率
k_values = np.arange(0, 0.271, 0.001)  # k值从0到0.27，步长为0.001
R_values = []  # 用于存储最优风险值
x_values = []  # 用于存储最优投资组合

# 对每个k值求解线性规划问题
for k in k_values:
    x0 = np.zeros(5)  # 初始投资组合

    # 约束条件
    cons = [
        {'type': 'ineq', 'fun': constraint_1, 'args': (k,)},
        {'type': 'eq', 'fun': constraint_2}
    ]

    # 目标函数最小化
    result = opt.minimize(objective, x0, args=(q,), constraints=cons, bounds=[(0, None)]*5)

    if result.success:
        # 记录最优风险和投资组合
        R_values.append(result.fun)
        x_values.append(result.x)
    else:
        # 无解的点跳过
        continue

# 剔除无解的点后，绘制k与最优解R的散点图
plt.figure(figsize=(8, 6))  # 调整图像大小
plt.scatter(k_values[:len(R_values)], R_values, color='blue', marker='o', alpha=0.6)

# 找到最优的点
if R_values:
    best_k_index = np.argmin(R_values)
    best_k = k_values[best_k_index]
    best_R = R_values[best_k_index]

    # 标注最优点
    plt.annotate(f'最优点: k={best_k:.3f}, R={best_R:.3f}', 
                 xy=(best_k, best_R), 
                 xytext=(best_k + 0.005, best_R + 0.005),
                 arrowprops=dict(facecolor='red', arrowstyle="->"),
                 fontsize=12, color='red')

# 添加图形标签
plt.xlabel('目标盈利水平 k', fontsize=12)
plt.ylabel('最优风险 R', fontsize=12)
plt.title('k与最优风险 R 的关系', fontsize=14)
plt.grid(True)
plt.show()

# 打印最佳k值和相应的最优解
if R_values:
    print(f"最优的k值为: {best_k}")
    print(f"对应的最优风险 R 为: {best_R}")
    print(f"对应的最优投资组合 x 为: {x_values[best_k_index]}")
else:
    print("没有找到有效的解")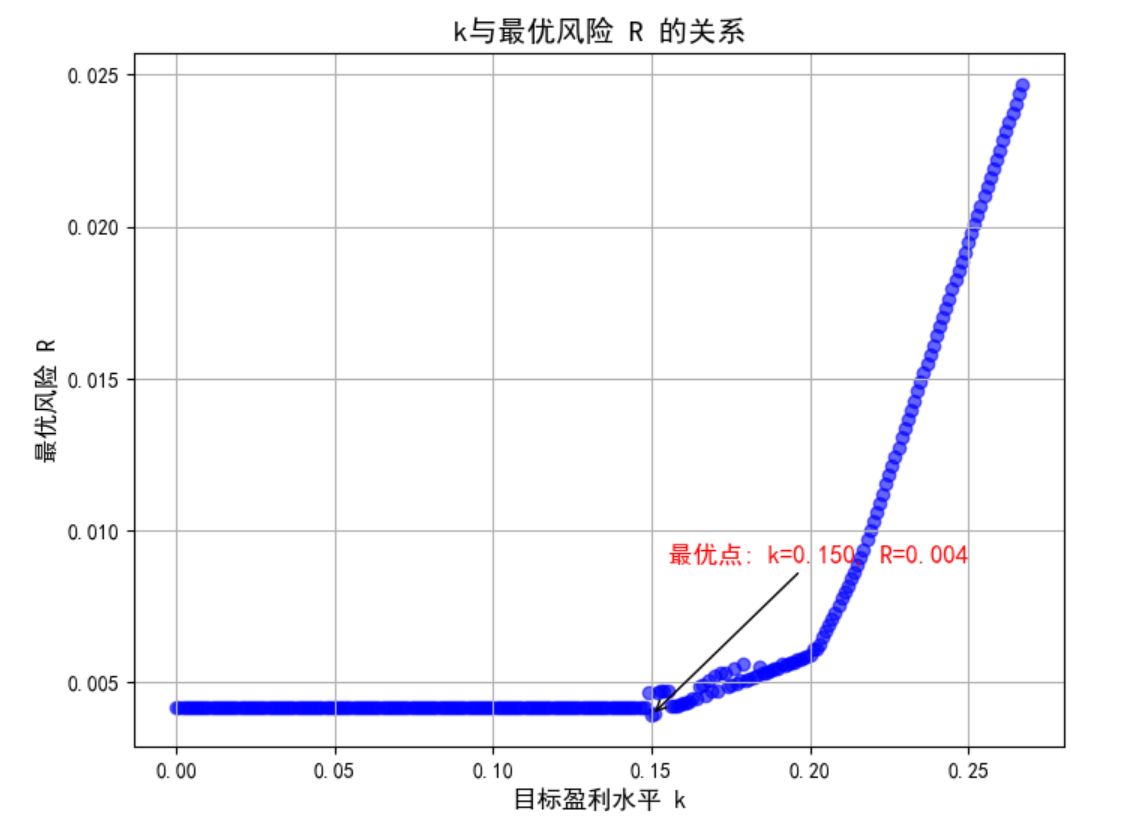

最优的k值为: 0.15
对应的最优风险 R 约为: 0.004
对应的最优投资组合 x 为: [0.34063082 0.15701512 0.26026417 0.07137367 0.15091922]

‍